SKEDSOFT

LOGICAL IMPLICATIONS: A proposition P (p, q, ……..) is said to logically imply a proposition Q (p, q,…….) written, P (p, q, ……..) → Q (p, q, …….) if Q (p, q, …….) is true whenever P (p, q, …….) is true.
Example  : P → (P ∨Q)

Solution : Consider the truth table for this

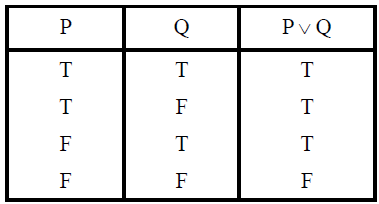
Observe that if P is true (T) in rows 1 and 2 then P∨ Q is also true (T) .
P → P ∨ Q.
If Q (p, q, …….) is true whenever P (p, q, …….) is true then the argument. P( p, q, ......) ├Q (p, q,......) is valid and conversely. i.e. the argument P├Q is valid iff the conditional statement P→Q is always true, i.e. a tautology.

Logical Equivalence Involving Implications : Let P & Q be two statements. The following table displays some useful equivalences for implications involving conditional and biconditional statements.

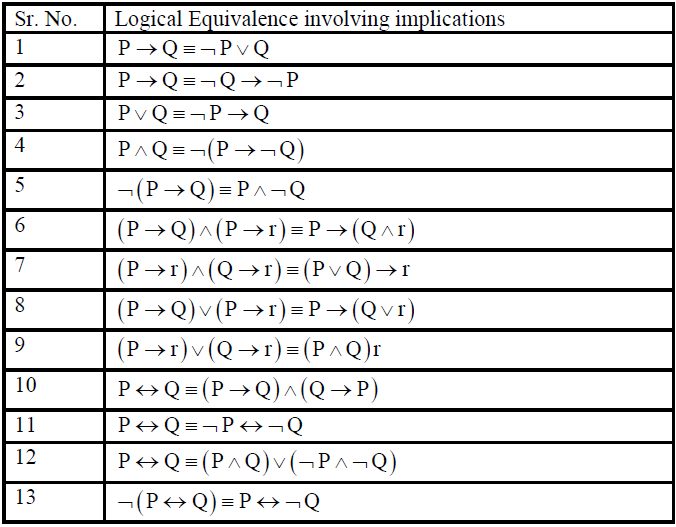
All these identities can be proved by using truth tables.