SKEDSOFT

The Five colour theorem: Every planar graph is 5-colorable.
Proof. We proceed by induction on the number P of points. For any planar graph having P ≤ 5 points, the result follows trivially since the graph is P-colorable.
As the inductive hypothesis we assume that all planar graphs with P points, P ≥ 5, are 5-colourable. Let G be a plane graph with P 1 vertices, G contains a vertex v of degree 5 or less. By hypothesis, the plane graph G – v is 5-colourable.
Consider an assignment of colours to the vertices of G – v so that a 5-colouring results, when the colours are denoted by Ci, 1 ≤ i ≤ 5.
Certainly, if some colour, say Cj, is not used in the colouring of the vertices adjacent with v, then by assigning the colour Cj to v, a 5-colouring of G results.
This leaves only the case to consider in which deg v = 5 and five colours are used for the vertices of G adjacent with v.
Permute the colours, if necessary, so that the vertices coloured C1, C2, C3, C4 and C5 are arranged cyclically about v, Now label the vertex adjacent with v and coloured Ci by vi, 1 ≤ i ≤ 5 (see Figure 2.100)

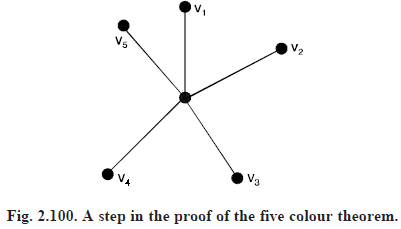
Let G13 denote the subgraph of G – v induced by those vertices coloured C1 or C3. If v1 and v3 belong to different components of G13, then a 5-coloring of G – v may be accomplished by interchanging the colors of the vertices in the component of G13 containing v1. In this 5-coloring however, no vertex adjacent with v is colored C1, so by coloring v with the color C1, a 5-coloring of G results.

If, on the other hand, v1 and v3 belong to the same component of G13, then there exists in G a path between v1 and v3 all of whose vertices are colored C1 or C3.
This path together with the path v1 vv3 produces a cycle which necessarily encloses the vertex v2 or both the vertices v4 and v5.

In any case, there exists no path joining v2 and v4, all of whose vertices are coloured C2 or C4. Hence, if we let G24 denote the subgraph of G – v induced by the vertices coloured C2 or C4, then v2 and v4 belong to different components of G24.

Thus if we interchange colors of the vertices in the component of G24 containing v2, a 5-colouring of G – v is produced in which no vertex adjacent with v is coloured C2. We may then obtain a 5-coloring of G by assigning to v the colour C2.