SKEDSOFT

ORE’S THEOREM : If G is a group with p ≥ 3 vertices such that for all non adjacent vertices u and v, deg u deg v ≥ p, then G is hamiltonian.
Proof. Let k denotes the number of vertices of G whose degree does not exceed n,

where  1 ≤ n ≤ p/2
These k vertices induce a subgraph H which is complete, for if any two vertices of H were not adjacent, there would exist two non adjacent vertices, the sum of whose degree is less than p.

This implies that k ≤ n 1. However k ≠ n 1, for otherwise each vertex of H is adjacent only two vertices of H, and if u ∈ V(H) and v ∈ V(G) – V(H), then deg u deg v ≤ n (p – n – 2) = p – 2, which is a contradiction.

Further k ≠ n ; otherwise each vertex of H is adjacent to at most one vertex of G not in H.

However, since k = n < p/2 , there exists a vertex w ∈ V(G) – V(H) adjacent to no vertex of H. Then if u ∈ V(H), deg u deg ω ≤ n (p – n – 1) = p – 1, which again a contradiction. Therefore k < n, which implies that G satisfies the condition, so that G is Hamiltonian.
Hence the proof.

Problem . Let G be a simple graph with n vertices and m edges where m is at least 3. If 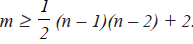Prove that G is Hamiltonian. Is the converse true ?
Solution. Let u and v be any two non-adjacent vertices in G. Let x and y be their respective degrees. If we delete u, v from G, we get a subgraph with n – 2 vertices. If this subgraph has q edges then q ≤ (1/2)(n – 2)(n – 3).
Since u and v are non-adjacent, m = q x y

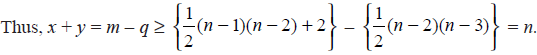
Therefore, the graph is Hamiltonian.
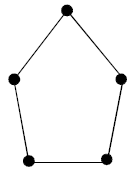
The converse of the result just proved is not always true. Because, a 2-regular graph with 5-vertices (see Figure below) is Hamiltonian but the inequality does not hold.