SKEDSOFT

PERMUTATION: On a finite set A of some objects, a permutation π is a one-to-one mapping from A onto intself.
For example, consider a set {a, b, c, d}.
A permutation π₁ = 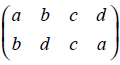takes a into b, b into d, c into c, and d into a. Alternating, we could write π1(a) = b, π1(b) = d, π1(c) = c, π1(d) = a.
The number of elements in the object set on which a permutation acts is called the degree of the permutation.
For example, the permutation π₁ = 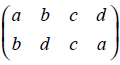is represented diagrammatically by Figure 6.7 below :

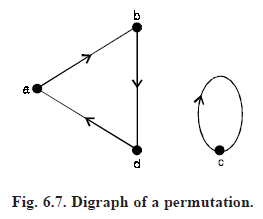
Permutation 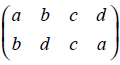can be written as (a b d) (c).
The number of edges in a permutation cycle is called the length of the cycle in the permutation.

A permutation π of degree k is said to be of type (σ1, σ2, ...... σk) if π has σi cycles of length i for u = 1, 2, ..... k.

For example, permutation is of type (2, 0, 2, 0, 0, 0, 0, 0).
Clearly, 1σ₁ 2σ₂ 3σ₃ ..... kσ_k = k.

COMPOSITION OF PERMUTATION
Consider the two permutations π1 and π2 on an object set {1, 2, 3, 4, 5} : π1 =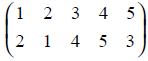
and π2 =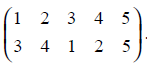
.
A composition of these two permutations π2π1 is another permutation obtained by first applying π1 and then applying π2 on the resultant.
That, is

π₂π₁(1) = π₂(2) = 4
π₂π₁(2) = π₂(1) = 3
π₂π₁(3) = π₂(4) = 2
π₂π₁(4) = π₂(5) = 5
π₂π₁(5) = π₂(3) = 1

Thus π2π1 =