SKEDSOFT

SUBGRAPH: A subgraph of G is a graph having all of its vertices and edges in G. If G1 is a subgraph of G, then G is a super graph of G1.

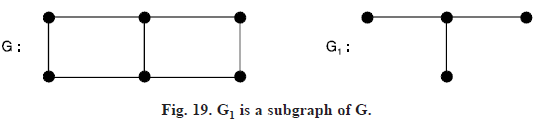
In other words. If G and H are two graphs with vertex sets V(H), V(G) and edge sets E(H) and E(G) respectively such that V(H) ⊆ V(G) and E(H) ⊆ E(G) then we call H as a subgraph of G or G as a supergraph of H.

Spanning subgraph: A spanning subgraph is a subgraph containing all the vertices of G. In other words, if V(H) ⊂ V(G) and E(H) ⊆ E(G) then H is a proper subgraph of G and if V(H) = V(G) then we say that H is a spanning subgraph of G. A spanning subgraph need not contain all the edges in G.

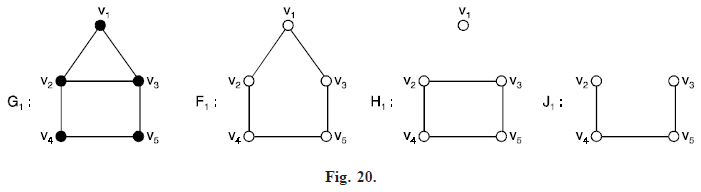
The graphs F1 and H1 of the above Fig. 20 are spanning subgraphs of G1, but J1 is not a spanning subgraph of G1.

Since V1 ∈ V(G1) – V(J1). If E is a set of edges of a graph G, then G – E is a spanning subgraph of G obtained by deleting the edges in E from E(G). In fact, H is a spanning subgraph of G if and only if H = G – E, where E = E(G) – E(H). If e is an edge of a graph G, then we write G – e instead of G – {e}. For the graphs G1, F1 and H1 of the Fig. 20, we have F1 = G1 – v2v3 and H1 = G1 – {v1v2, v2v3}.

Removal of a vertex and an edge: The removal of a vertex vi from a graph G result in that subgraph G – vi of G containing of all vertices in G except vi and all edges not incident with vi. Thus G – vi is the maximal subgraph of G not containing vi. On the otherhand, the removal of an edge xj from G yields the spanning subgraph G – xj containing all edges of G except xj. Thus G – xj is the maximal subgraph of G not containing xj.

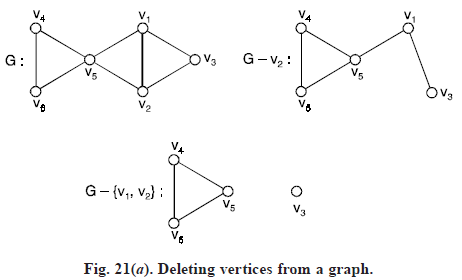
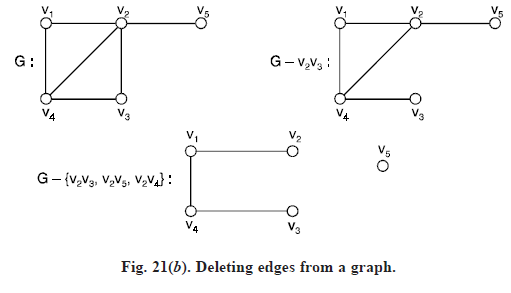
Induced subgraph: For any set S of vertices of G, the vertex induced subgraph or simply an induced subgraph <S> is the maximal subgraph of G with vertex set S. Thus two vertices of S are adjacent in <S> if and only if they are adjacent in G. In other words, if G is a graph with vertex set V and U is a subset of V then the subgraph G(U) of G whose vertex set is U and whose edge set comprises exactly the edges of E which join vertices in U is termed as induced subgraph of G.

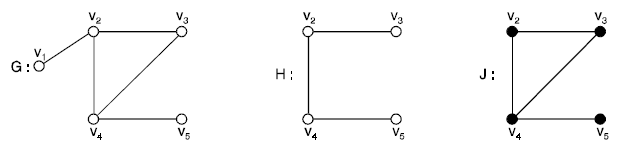
Here H is not an induced subgraph since v4v1 ∈ E(G), but v4v3 ∉ E(H). On the otherhand the graph J is an induced subgraph of G. Thus every induced subgraph of a graph G is obtained by deleting a subset of vertices from G.
Note : Let | V | = m and | E | = n. The total non-empty subsets of V is 2^m – 1 and total subsets of E is 2ⁿ. Thus, number of subgraphs is equal to (2^m – 1) × 2ⁿ. The number of spanning subgraphs is equal to 2ⁿ.