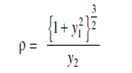SKEDSOFT

Radius of Curvature:

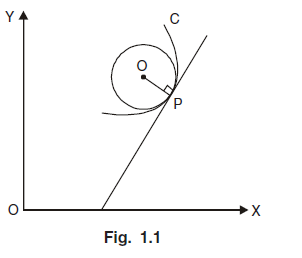
Let Pbe any point on the curve C. Draw the tangent at Pto the circle. The circle having the same curvature as the curve at P touching the curve at P, is called the circle of curvature. It is also called the osculating circle. The centre of the circle of the curvature is called the centre of curvature. The radius of the circle of curvature is called the radius of curvature and is denoted by ‘ρ’.

Note : 1. If k (> 0) is the curvature of a curve at P, then the radius of curvature of the curve of ρ is 1/k. This follows from the definition of radius of curvature and the result that the curvature of a circle is the reciprocal of its radius.

Note : 2. If for an arc of a curve, ψ decreases as s increases, then dψ/ds is negative, i.e., k is negative. But the radius of a circle is non-negative. So to take ρ = 1/|k| = |ds/dψ| some authors regard k also as non-negative i.e., k = |dψ/ds|. The sign of dψ/ds indicates the convexity and concavity of the curve in the neighbourhood of the point. Many authors take ρ = ds/dψ and discard negative sign if computed value is negative.

∴ Radius of curvature ρ = 1/|k|·

Radius of Curvature in Cartesian Form:

Suppose the Cartesian equation of the curve C is given by y = f (x) and A be fixed point on it. Let P (x, y) be given point on C such that arc AP = s. Then we know that,

Where ψ is the angle made by the tangent to the curve C at point P with the x - axis and

Differentiate (1) w.r.t x, we get

Hence equation (3) becomes;