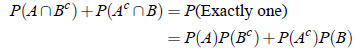SKEDSOFT

Addition Theorem of Probability:

If A₁,A₂, . . . , A_k be k mutually exclusive events on a sample space associated with a random experiment, then the probability of happening one of them is the sum of their individual probabilities. In symbols,

             P(A1 A2 . . . Ak) = P(A1) P(A2) . . . P(Ak)
or
             P(A1 ∪ A2 ∪. . .∪ Ak) = P(A1) P(A2) . . . P(Ak)

Proof: Let total ways = N. Let a₁,a₂, . . . ,ak be the favorable ways to the events A₁,A₂, . . . ,A_k respectively. Then the number of favorable ways to any one of the events = a₁ a₂ . . . a_k

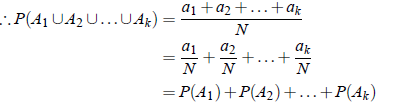
Conditional Probability:

The probability that the event B will occur, it being known that A has occurred is called the conditional probability of B and is denoted by P(B/A).In symbols,

Conditional probability of B when A has happened =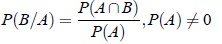 

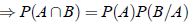
Multiplication Theorem of Probability:

1. The probability of happening of the two independent events A and B together is equal to the product of their individual probabilities. That is

               P( A ∩ B = P(A) P(B )

2. If A and B are not independent, then the probability P( A ∩ B ) of their simultaneous occurrence is equal to the product of the probability of A, P (A) and the conditional probability P (B/A). In symbols

              P( A ∩ B ) = P (A) P(B/A)
or
              P( A ∩ B ) = P(B) P(A/B)

Specific Formulas:

1. If P( A ∩ B ) = P(A) P(B), then

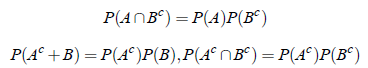
2. If the events A and B are independent

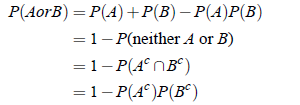
3. If the events A and B are independent