SKEDSOFT

BCS theory and Cooper pairs: According to classical physics, part of the resistance of a metal is due to collisions between free electrons and the crystal lattice’s vibrations, known as phonons. In addition, part of the resistance is due to scattering of electrons from impurities or defects in the conductor. As a result, the question arose as to why this does not happen in superconductors?
A microscopic theory of superconductivity was developed in 1957 by John Bardeen, Leon Cooper and J. Robert Schrieffer, which is known as the BCS theory. The central feature of the BCS theory is that two electrons in the superconductor are able to form a bound pair called a Cooper pair if they somehow experience an attractive interaction between them. This notion at first sight seems counterintuitive since electrons normally repel one another because of their like charges. This may be thought of in the following way and is illustrated in Figure 1.

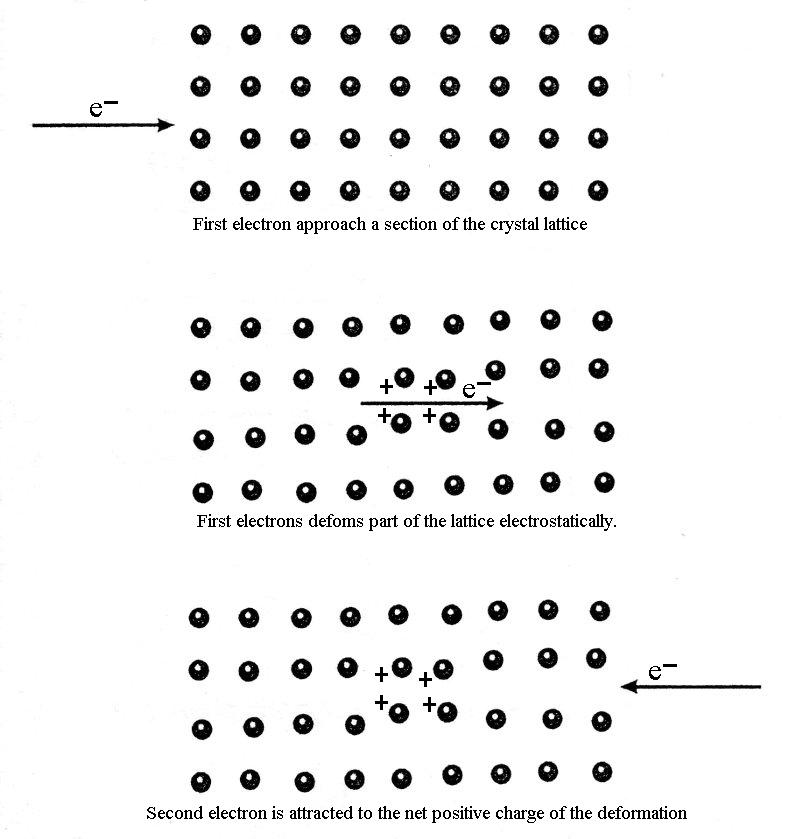
Figure 1. Classical description of the coupling of a Cooper pair.

An electron passes through the lattice and the positive ions are attracted to it, causing a distortion in their nominal positions. The second electron (the Cooper pair partner) comes along and is attracted by the displaced ions. Note that this second electron can only be attracted to the lattice distortion if it comes close enough before the ions have had a chance to return to their equilibrium positions. The net effect is a weak delayed attractive force between the two electrons.

This short lived distortion of the lattice is sometimes called a virtual phonon because its lifetime is too short to propagate through the lattice like a wave as a normal phonon would.
From the BCS theory, the total linear momentum of a Cooper pair must be zero. This means that they travel in opposite directions as shown in Figure 1. In addition, the nominal separation between the Cooper pair (called the coherence length) ranges from hundreds to thousands of ions separating them! This is quite a large distance and has been represented incorrectly in many textbooks on this subject. If electrons in a Cooper pair were too close, such as a couple of atomic spacings apart; the electrostatic (coulomb) repulsion will be much larger than the attraction from the lattice deformation and so they will repel each other. Thus there will be no superconductivity. A current flowing in the superconductor just shifts the total moment slightly from zero so that, on average, one electron in a cooper pair has a slightly larger momentum magnitude that its pair. They do, however, still travel in opposite directions.
The interaction between a Cooper pair is transient. Each electron in the pair goes on to form a Cooper pair with other electrons, and this process continues with the newly formed Cooper pair so that each electron goes on to form a Cooper pair with other electrons. The end result is that each electron in the solid is
attracted to every other electron forming a large network of interactions. Causing just one of these electrons to collide and scatter from atoms in the lattice means the whole network of electrons must be made to collide into the lattice, which is energetically too costly. The collective behaviour of all the electrons in the solid prevents any further collisions with the lattice. Nature prefers situations that spend a minimum of energy. In this case, the minimum energy situation is to have no collisions with the lattice. A small amount of energy is needed to destroy the superconducting state and make it normal. This energy is called the energy gap.

Although a classical description of Cooper pairs has been given here, the formal treatment from the BCS theory is quantum mechanical. The electrons have wave-like behaviour and are described by a wave function that extends throughout the solid and overlaps with other electron wave functions. As a result, the whole network of electrons behaves line one wave function so that their collective motion is coherent.
In addition to having a linear momentum, each electron behaves as if it is spinning. This property, surprisingly, is called spin. This does not mean that the electron is actually spinning, but behaves as though it is spinning. The requirement from the BCS theory is that spins of a Cooper pair be in opposite directions.
Note that the explanation and pictorial representation of a Cooper pair presented here comes directly from BCS theory. However, current HSC textbooks tend to distort this picture with unphysical situations such as the Cooper pair being within one or two atomic spacings and traveling in the same direction – each of
these situations is false.