SKEDSOFT
Phase and group velocity: To understand the difference between phase and group velocity of waves, consider the following analogy. A group of people, say city marathon runners, start from the starting at the same time. Initially it would appear that all of them are running at the same speed. As time passes, group spreads out (disperses) simply because each runner in the group is running with different speed. If you think of phase velocity to be like the speed of individual runner, then the group velocity is the speed of the entire group as a whole. Obviously and most often, individual runners can run faster than the group as a whole. To stretch this analogy, we note that the phase velocity of waves are typically larger than the group velocity of waves. However, this really depends on the properties of the medium. Briefly, phase velocity refers to a monochromatic wave, let’s say, the velocity of one of the peaks of the wave. For example, a monochromatic wave with angular frequency ω = 2πν (ν is the frequency) travelling in ve x-direction is given by,
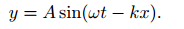
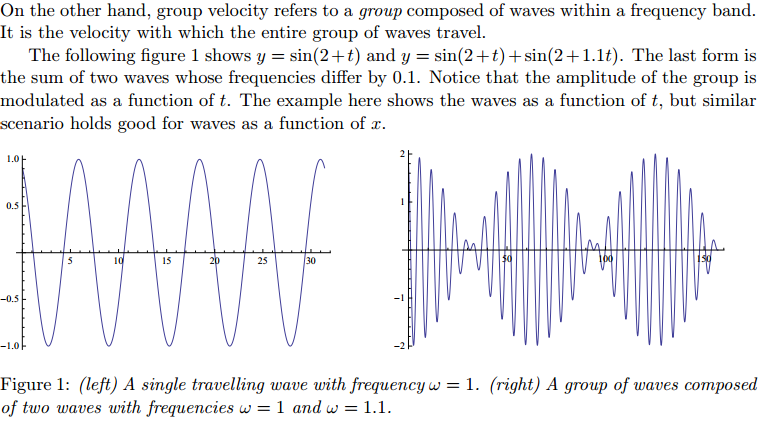
In quantum physics, a group of waves can be associated with a material particle (De Broglie’s hypothesis). If the particle is moving with speed v << c, then the wavelength of wave group associated with the particle is λ = h/mv, where h is Planck’s constant. If y(x) represents one such wave group, then |y(x)| 2
gives the probability density for ï¬nding the particle in the range x and x dx. Further, it can also be shown that the group velocity vg = v. Since the information
on the position and velocity of the particle can be obtained from y(x), this represents the state of the particle.