Time Varying Field

Time Varying Field: Even where there is no relative motion between an observer and a conductor, an emf (and consequently an induced current for a closed conducting loop) may be induced if the magnetic field itself is varying with time as flux change may be effected by change in magnetic field with time. In effect it implies that a changing magnetic field is equivalent to an electric field in which an electric charge at rest experiences a force.
Consider, for example, a magnetic field $\vec B$ whose direction is out of the page but whose magnitude varies with time. The magnetic field fills a cylindrical region of space of radius . Let the magnetic field be time varying and be given by

$\begin{displaymath}B =\left\{ \begin{array}{l} B_0\sin\omega t\ \ {\rm for}\ r\le R\\ 0\ \hspace{10mm}{\rm for} \ \ r>R \end{array}\right. \end{displaymath}$

Since $\vec B$ does not depend on the axial coordinate as well as the azimuthal angle $\phi$ , the electric field is also independent of these quantities. Consider a coaxial circular path of radius $r\le R$ which encloses a time varying flux. By symmetry of the problem, the electric field at every point of the cicular path must have the same magnitude and must be tangential to the circle.

Thus the emf is given by $\begin{displaymath}{\cal E} = \int\vec E\cdot\vec{dl}= 2\pi r E\end{displaymath}$

By Faraday's law $\begin{eqnarray*} {\cal E} &=& -\frac{d\Phi}{dt} = -\frac{d}{dt}[\pi r^2B(t)]\\ &=& -\pi r^2 \frac{dB(t)}{dt} \end{eqnarray*}$

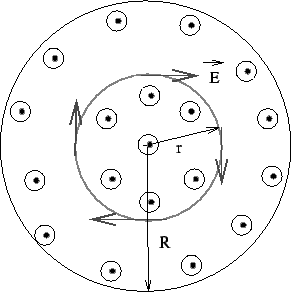
Equating these, we get for $r\le R$ , $\begin{displaymath}E = -\frac{r}{2}\frac{dB}{dt} = -\frac{B_0\omega}{2}r\cos\omega t\end{displaymath}$

For , the flux is $\Phi = \pi R^2B(t)$ , so that $\begin{displaymath}{\cal E} = -\frac{d\Phi}{dt} = -\pi R^2\frac{dB}{dt}\end{displaymath}$

and the electric field foir is $\begin{displaymath}E = -\frac{R^2}{2r}\frac{dB}{dt} = -\frac{B\omega R^2}{2r}\cos\omega t\end{displaymath}$

SKEDSOFT