SKEDSOFT
Single Sampling OC Curves:
Example(Transportation Safety Inspections)
An airport operator is considering using video surveillance to evaluate a team of trainees with respect to courteous and effective safety checks of passengers. (This is a case of inspecting inspectors.) The airport has only enough resources to examine surveillance tape for 150 passengers out of the 2000 inspections that occur each day. If greater than three inspections are unacceptable discourteous and/or ineffective, the entire team is flagged for re-training. Plot the OC curve for this policy and briefly describe the implications.
Answer:This question is based on a single sampling plan for N = 2000 units in a lot. It has n = 150 units in a sample and the rejection limit is c = 3.
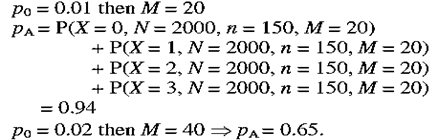
The plot shows that the single sampling approach will effectively identify trainees yielding unacceptable inspections greater than 5% of the time, and if the fraction nonconforming is kept to less than 1%, there is almost zero chance of being found to need re-training.
Double Sampling OC curves:
The event that a double sampling procedure results in acceptance is relatively complex. Denote the number of units found nonconforming in the first set of inspections as X1 and the number found nonconforming in the optional second set of inspections as X2. Then, the acceptance occurs if {X1 ≤ c1} or if {c1 < X1 ≤ r and X1 X2 ≤ c2}. Therefore, the double sampling probability of acceptance is:
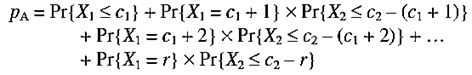
This is expressed in terms of cumulative hyper geometric probabilities for assumptions that might be considered reasonable. Advanced readers will notice that the assumption of independence of X1 and X2 is implied by the above equation. Because of the computational challenge, it is common to apply the binomial approximation and the binomial cumulative when it is appropriate.